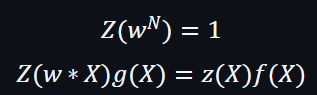一個向量中，可以證明多個不同位置上的向量元素相等，例子如下: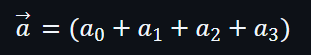
如果要證明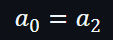
可以將它們的位置對調，以σ 表示位置向量: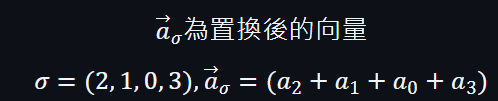
只要Prover證明到置換前的向量和置換後的向量相等，就表示:
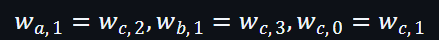
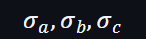
因此，現在會有2個向量，分別是置換前的向量及置換後的向量。為了進行下一步驗證，需要利用一個隨機數β來進行向量合併。
之後再利用另一個隨機數γ配合連乘以獲得2個向量的Multisets。
置換前的向量: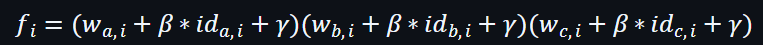
置換後的向量: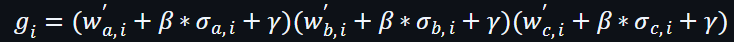
進一步演示 - 置換前的向量: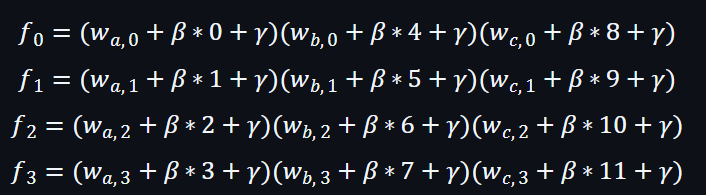
進一步演示 - 置換後的向量: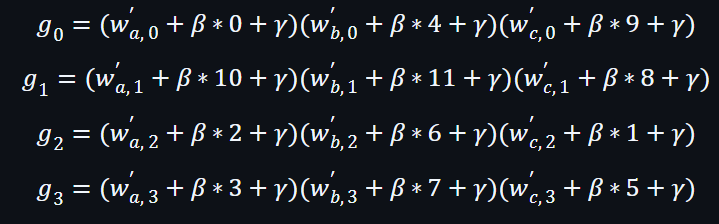
由於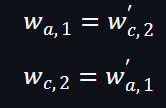
所以: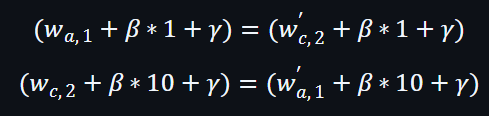
換言之: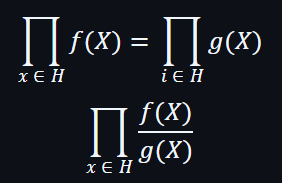
現在再利用新的向量z，以表示連乘計算的一系列中的過程。
需假設: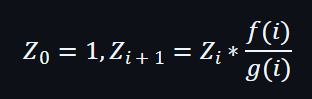
Prover可以計算出以下的值:
所以: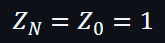
另外，由於: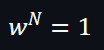
所以:
iThome鐵人賽
看影片追技術